前回は費用対効果の立式について解説しました。本稿では投資対効果の立式についてみていきます。定義を再掲すると、投資対効果は「短期的な効果に加え、出稿終了後も中長期に渡って発揮され比較的緩やかに減衰していく効果を合わせたROI」を表します。費用対効果と投資対効果の使い分けについて詳しくは、費用対効果と投資対効果の違いをご覧下さい。
投資対効果の立式:広告やクロスメディアの中長期的な効果に対するROI
広告の”投資”としての側面は、「将来のリターンを期待して、”今”費用を投下する」事です。しかしブランドを育成したりロイヤルティを高めたりという事は一朝一夕でできる事ではありません。その意味で、費用対効果の立式で登場した(14)式
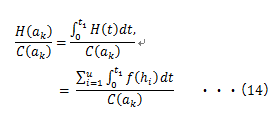
は、マス4媒体やソーシャルメディア等のROI算出には不向きな面があります。何故かと言うと、それら媒体の広告効果は、行ってすぐリターンとして得られる部分と、必ずしもすぐには得られない部分があるからです。例えば前者はTVCMの認知率を増加させる効果、後者はTVCMのブランドを作る効果が挙げられます。
(14)式はt1期までに得られたリターンで計算している一方、t1期以降で発生するリターンが分子に入っていません。しかし本来、現在行っている(もしくはこれから行おうとしている)マーケティングコミュニケーションのROIを考える際には、「将来的に回収する事が期待できる全てのリターンと、その為に現在行う投資の効率性を考える」のが自然です。
特にマス4媒体やソーシャルメディア、オウンドメディアなどを含むクロスメディアからは短期的な効果に加え、中長期的な効果も発現します。古川、守口、阿部ら(2003)では、平均的にみると広告の長期的効果は短期的効果の約4.5倍という報告もあり、今得られているリターンだけで(14)式のROIを計算すると、「投資対効果」としては過小評価になる恐れがあります。その場合、「今回幾ら使って、”将来含め”トータルで幾ら返ってくるのか」という将来のキャッシュフローも含めた投資対効果を計算します。
まず、投資対効果の分子を考えます。投資対効果は短期的な効果と長期的な効果の両方を考えますので、(11)式を再掲します。
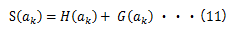
(11)式の右辺第二項は将来的に発生するキャッシュフローを表していますので、投資対効果を計算する際は現在価値に割り引く必要があります。
従って、(11)式を書き直して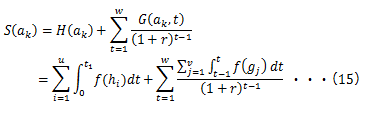
を得ます。rは割引率です。(15)式の右辺第二項は広告akのj番目の長期効果gjの増分リターンを期ごとに合計し、現在価値に割り戻した値をtw期まで累計しています(※1)。会計やファイナンスをされた方は見慣れた式だと思いますが、将来に渡り発生する長期効果のキャッシュフローの総和の現在価値を表すDCFです。(15)式におけるtは、何期先までのキャッシュフローを計算するかという演算子の役割も担っています。この「何期先までリターンが期待できるのか?」という問いに答えるには、広告の残存効果を考える必要があり、後程説明していきます。
従って投資対効果は、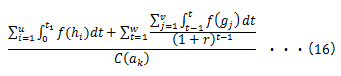
と表す事ができます。
投資対効果の場合、ROIを計算しようとしている時点では売上が立っていないので、まず売上予測を行う必要があります。利益ベースで算出する際にも、売上予測を行った上で利益計算を行います。ファイナンスでよく用いられる方法は、過去の確定している売上高などから成長率を算出し、その成長率に従って時系列的に予測する方法です。移動平均や指数平滑、成長曲線、自己回帰モデルなど色々ありますが、基本的な考え方は、過去から現在までの平均的な成長を将来にも期待して売上を算出する事です。マーケティングサイエンスでは、売上に影響する要因の関数を用いて予測を行うモデルも利用します。例えば、耐久消費財ならバースモデル、FMCGならトライアルリピートモデルなどが有名です。
既存品やブランドエクステンションの場合、前者、つまり過去の実績データや類似ブランドの売上データを使って簡便的に売上予測を立てる事ができます。後者は特に、「売上予測+シミュレーション」を行う時に役立ちます。例えば、売上を広告投下量や媒体配分、クリエイティブの関数で表現できる予測モデルを組めば、出稿計画をシミュレーションしながらROIの変化を推論し、影響要因を特定していく事に繋がります。
残存効果の推定
売上予測を行った後で、その予測額の中から現在行う広告に由来するリターンを割り出す必要があります。これは費用対効果の立式時と同様に広告効果の分解を行うのですが、投資対効果の場合それに加えて、広告の残存効果をフォローしなければいけません。広告効果はどうしても時間の経過と共に減っていくので、その減衰率をモデリングして時間経過に伴い将来分のリターン推定値自体を下方修正する作業が必要になるからです(※2)。
古川、守口、阿部ら(2003)では、約100の調査をメタ分析して得られた平均的な月次の減衰率(λ)が0.775になったと報告されています。以下の図は、筆者らにならい広告の効果減衰の様子をλ=0.775としてシミュレーションしたものです。横軸が時間の経過、縦軸が広告効果です。
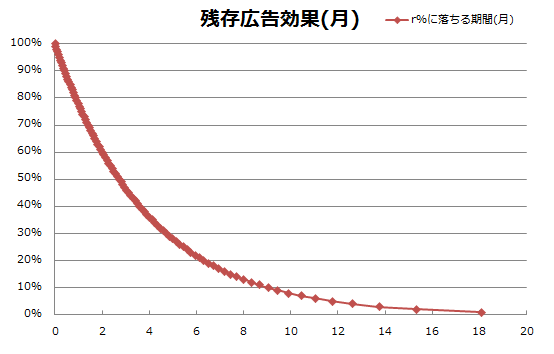
グラフから、出稿当初の広告効果を100%として時間の経過と共に効果は減衰していき、約3ヶ月で効果は半減、半年で最初の20%程度、1年で最初の5%程度、1年半も経つと残存効果はほとんど無くなる事が読み取れます(※3)。
実際の分析においては様々な効果減衰パターンが想定できます。本来は媒体やクリエイティブの特性に応じて適切な減少関数を構成し、(16)式の分子を調整するべきです。しかし広告効果が継時的に一定の割合で単調減少すると仮定できれば、その様子は等比数列で容易にモデル化できます。その場合、計量経済学にコイック型モデルという、過去の広告量をラグ項として用いて売上を広告の短期効果と効果減衰率の関数として表現する回帰式があり、それを利用することできます。最初にROIに取り組むときは、個別媒体の反応関数をあまり複雑にすると後で積分が大変になるので、多少精度を犠牲にしてもシンプルなモデルからスタートする事をお勧めします。
複数の媒体を用いている場合、媒体ごとに減衰率は異なりますので各媒体ごとに分析する必要がありますが、媒体ごとの残存効果を知ることで、どの媒体だと何期先までのリターンを計算するべきかという演算子tについてノウハウを蓄積することができます。
※1 基本的にf(gj)は長期効果であり短期即時的に売上に貢献する事を期待する効果ではありませんので、ここではまとめてt1から積分していますが、t0-t1の閉区間にも効果が発現すると想定する事が自然なgjについてはその限りではありません。この辺りは個別のケースごとに判断する事になります。
※2 割引率(r)と減衰率(λ)は異なります。割り引くというのは将来に発生する価値を現在の価値に割り戻すことです。減衰率は、時間と共に減っていく広告効果自体を推定する為に必要になります。例えば、「インパクトの強いTVCMを見ても、時が経てばそのインパクトも薄れていく様子」をモデリングするイメージです。
※3 この残存効果の推定値は、様々な研究調査のメタ分析によるものなので、全ての広告の月次減衰率としてただちに一般化できるわけではありません。




